Welcome to Game Theory's Trilogy for the Leaders of Tomorrow

"WarGames" is a 1983 film directed by John Badham and starring a young Matthew Broderick. Set during the height of the Cold War, it tells the story of a high school student who hacks into the U.S. military's central computer, which is capable of starting a nuclear war.

Those of us who grew up in the 80s and enjoyed the movie "WarGames" will remember how David and Jennifer, after initially stumbling upon what seemed like a video game company, encounter "Joshua," an artificial intelligence trained over the years in different strategy games (Chess, Checkers, Poker, etc.) by Dr. Stephen Falken.

Without giving away any spoilers, today, after years of training various artificial intelligences developed by brilliant but less tormented minds than Dr. Falken's, we now have, for example, chess engines so powerful that if we play as mere humans, defeat is almost inevitable.

At this point, we might ask ourselves: Is it still worth playing chess, given that even international competitions are being questioned? Should we now delegate decision-making entirely to artificial intelligences trained for this purpose? Can we do anything more than just watch? And if we only observe, are we sure that letting an artificial intelligence run on autopilot is the best option? These are questions we ask ourselves every day now, but they were already being raised back in 1983 with the release of "WarGames," as many of us remember.

"Moneyball" is a 2011 film directed by Bennett Miller and starring Brad Pitt. Set in the world of professional baseball, it follows the story of Billy Beane, the Oakland A's general manager, who revolutionizes the game by using data and statistical analysis to assemble a competitive team on a limited budget.

It's fascinating to see how, in this new era of artificial intelligence, where new applications and innovations are presented to us daily, we're encouraged to invest in and support the leading companies in the sector and we're gradually being nudged into accepting that decisions can be made by algorithms we don't fully understand. Yet, in business leadership, we still seem bound to decision-making models shaped by phrases like "this is how it's always been done" ,"the boss requested it" or "the competition is doing it". Even when we take the time to apply some math, we often resort to static and overly complex Excel based business plans sold at a premium by consultants, these Excels feel more like playing a game of Risk trying to gain just 5% more territory with each turn.

Unfortunately, it's all too common for many business decisions to be made in the following way: First, different assumptions or hypotheses are formed, and then conclusions are drawn, skipping the critical step that Game Theory covers, which is doing the right math before make any decision. Indeed, Game theory provides a rigorous framework that ensures our conclusions follow logically from the assumptions we make.

So, why is it that in the age of artificial intelligence, we still make decisions without doing the right math? It's certainly a difficult question to answer. However, one question we will try to address is this: Can we make better decisions to become better leaders?

When starting out with Game Theory, one often encounters the classic Prisoner's Dilemma. However, in keeping with the theme of leadership in the business world, we'll adjust the context to reflect a more relevant scenario the Duopoly Dilemma. In this Dilemma, two dominant payment companies, face accusations from regulators for abusing their market power. Although there’s little evidence, each company could receive a fine for data misuse. However, if one reports the other, they are exonerated and gain market share, while the accused faces heavy penalties. If both accuse each other, they both suffer severe penalties. If neither reports, both receive smaller fines due to lack of proof. The dilemma mirrors the classic Prisoner’s Dilemma betrayal offers a personal advantage, but mutual defection leads to a worse outcome for both, forcing each to weigh their self-interest against cooperation.

In this situation, a leader might assume that avoiding cooperation with the regulator is the best choice, believing both companies will gain more by staying silent. However, the math proves otherwise. Game theory shows that this strategy often leads to worse outcomes for both companies, highlighting that non-cooperation is rarely the optimal decision.

In this matrix, each player has two options: to keep quiet or confess. The dominant strategy here is for both players to confess. This is because, regardless of what Player 1 does, Player 2 minimizes their loss by confessing (0 > -1 & -8 > -12), and same for Player 1.

"A Beautiful Mind" is a 2001 film directed by Ron Howard and starring Russell Crowe as John Nash, a brilliant mathematician. The movie delves into Nash’s groundbreaking work in game theory, particularly the concept of Nash Equilibrium, which revolutionized economics and strategic decision-making.

Game Theory is a mathematical framework for understanding strategic decision-making. It analyzes how individuals, businesses, or even nations make decisions in situations where the outcome depends on the choices of others. At its core, provides insights into how rational players can anticipate the actions of others and optimize their strategies accordingly. The key elements are players, strategies, and payoffs. Players have different strategies available, and the results (or payoffs) depend on the choices made by both themselves and other players.

One of the fundamental concepts is the Nash Equilibrium, where no player can gain by changing their strategy if the others remain constant. This equilibrium often explains why certain competitive outcomes are stable, even if they are not the most beneficial for all parties involved.

Game Theory can be applied in countless fields such as economics, politics, business, and artificial intelligence. It provides valuable tools for analyzing markets and negotiations by modeling competition and cooperation in a structured way. By understanding the underlying incentives and potential outcomes, Game Theory helps leaders make more informed decisions, paving the way for strategies that account for the actions and reactions of others in competitive environments.

In Game Theory, a zero-sum game is a situation where the gain of one player is exactly equal to the loss of another player. This means that the total "sum" of outcomes across all players always equals zero. These games are typically competitive, with examples ranging from board games like Chess to real-world markets where companies compete for market share. In such a scenario, one company’s gain results in an equal loss for the competitor.
Meanwhile a perfect information game is a game where all players have complete knowledge of the game state at all times. Chess is a famous example of this. At any point during the game, both players know the exact configuration of the board and all previous moves. There are no hidden elements or randomness, unlike games like Poker, where players do not know the cards in their opponent's hands. This distinction makes strategic planning highly crucial in games of perfect information

In zero-sum games like Chess, the combination of the Minimax Algorithm and Alpha-Beta Pruning allows players (and AI systems) to make optimized, strategic decisions. These techniques ensure that players can anticipate their opponent's best possible moves and make the most informed decisions.

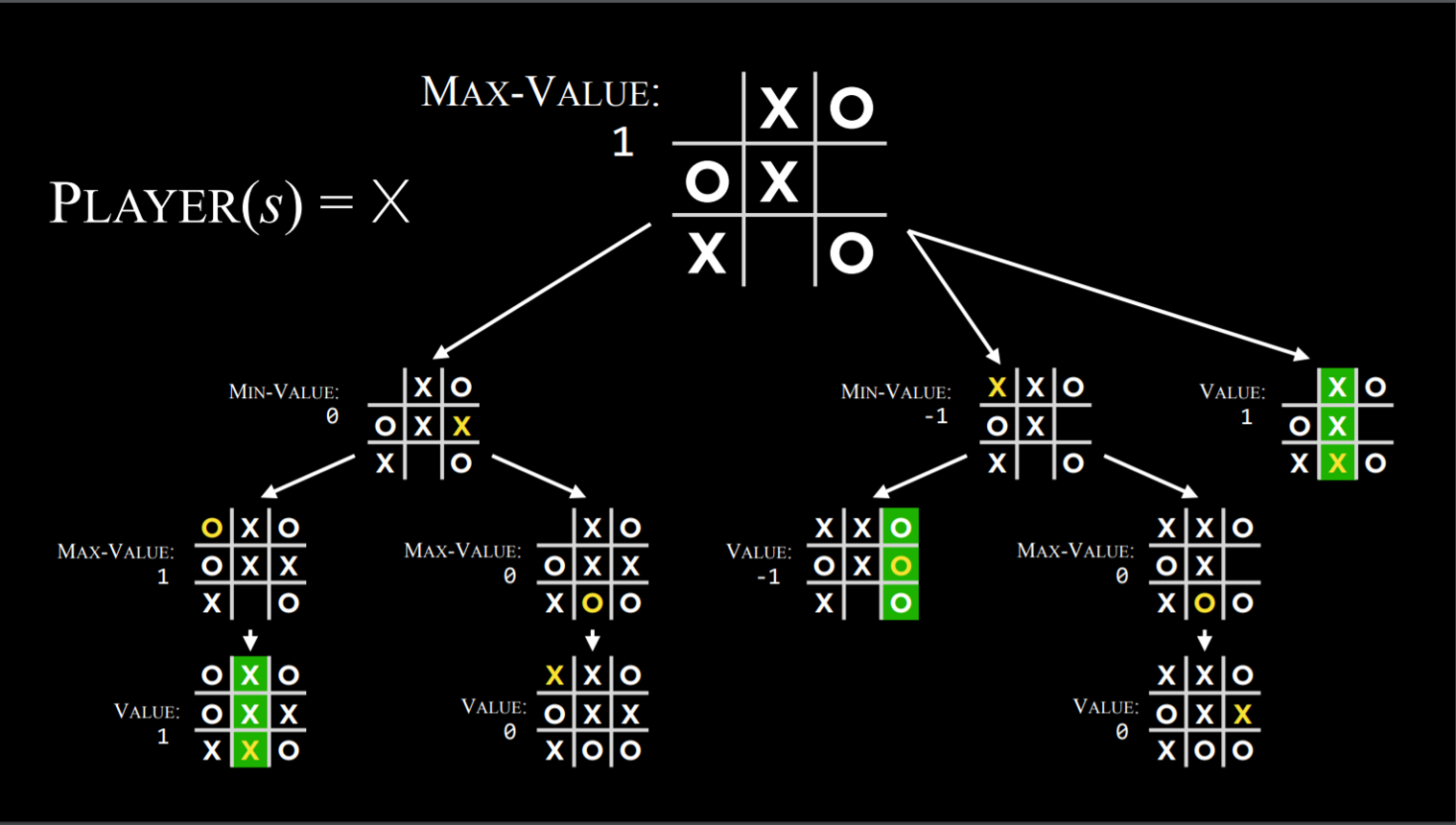
The Minimax Algorithm is a key decision-making algorithm in perfect information, zero-sum games. It operates under the assumption that both players will play optimally, meaning each will make the best possible move to maximize their gains while minimizing the other's. In a game like Chess, this results in players considering all possible moves and responses to find the optimal strategy, which ensures the best possible outcome in the worst-case scenario.

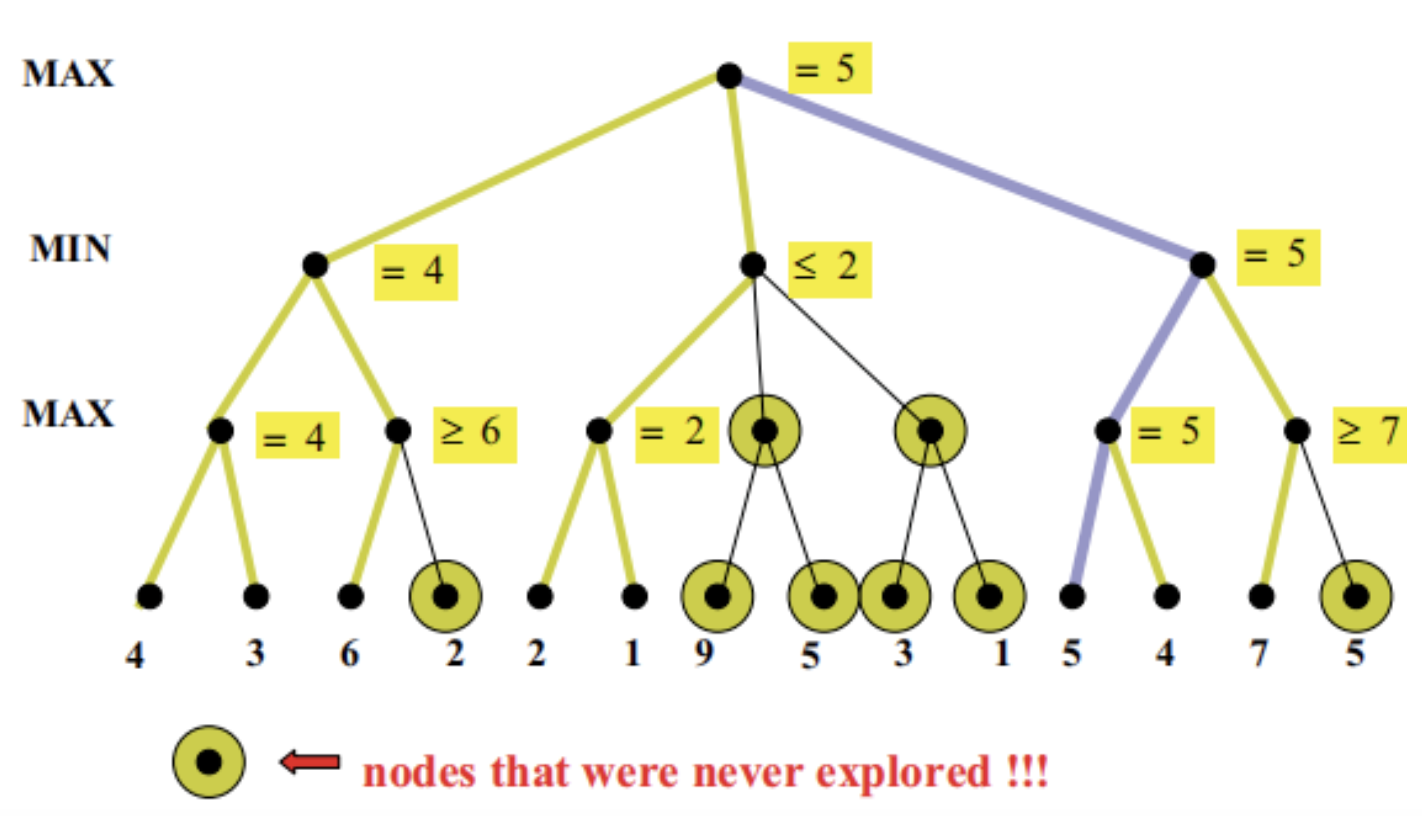
Alpha-Beta Pruning is an optimization technique that improves Minimax by reducing the number of nodes evaluated in the game tree. It "prunes" branches of the tree that do not influence the final decision. This technique is essential for complex games like Chess, where there are vast numbers of possible moves. By pruning irrelevant branches, Alpha-Beta Pruning allows the algorithm to explore deeper into the game, making it computationally feasible to analyze several moves ahead, similar to how grandmasters play.

MinMax and Alpha-Beta Pruning have been pivotal in the evolution of AI decision-making strategies. Both algorithms have enabled AI systems to handle complex, strategic decision-making in games by analyzing several possible future moves and counter-moves, which makes the AI excel in planning, reasoning, and adapting to opponents’ strategies.

Key AI Milestones:
Deep Blue vs. Garry Kasparov (1997) Context: Deep Blue became the first AI to defeat a world chess champion, Garry Kasparov. How: MinMax and Alpha-Beta Pruning allowed Deep Blue to evaluate millions of positions per second by focusing on the most promising moves and pruning irrelevant ones.
AlphaGo vs. Lee Sedol (2016)
Context: AlphaGo, by Google DeepMind, defeated Go champion Lee Sedol in a five-game series. How: Combining MinMax, Alpha-Beta Pruning, and Monte Carlo Tree Search (MCTS), AlphaGo navigated Go's vast move possibilities to make superior strategic choices.

In conclusion, in zero-sum games like Chess as we will see in the next chapter, the combination of the Minimax Algorithm and Alpha-Beta Pruning allows players (and AI systems) to make optimized, strategic decisions.

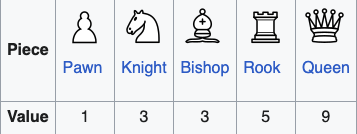
In BattleChess, the AI's decision-making begins with assigning numerical values to each chess piece. These values represent the relative strength and importance of the pieces, allowing the AI to quantify material advantages or disadvantages during the game.

The standard valuations used are:

The oldest derivation of the standard values is due to the Modenese School (Ercole del Rio, Giambattista Lolli, and Domenico Lorenzo Ponziani) in the 18th century and is partially based on the earlier work of Pietro Carrera.The value of the king is undefined as it cannot be captured, let alone traded, during the course of the game

Chess engines usually assign the king an arbitrary large value such as 200 points or more to indicate that the inevitable loss of the king due to checkmate trumps all other considerations. The endgame is a different story, as there is less danger of checkmate, allowing the king to take a more active role.

These values are fundamental for the evaluation. For instance, if you capture an opponent's bishop (3 points) in exchange for a knight (3 points), the balance remains equal. However, capturing a rook (5 points) for a bishop (3 points) gives you a material gain of 5 - 3 = +2 points.

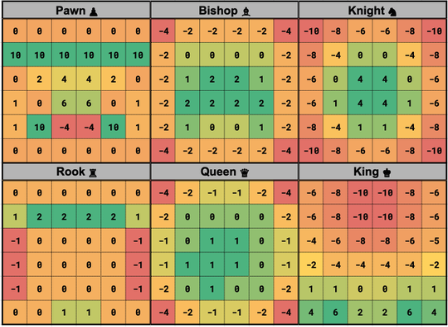
Beyond assigning numerical value to the pieces, the AI evaluates the positions of the pieces using Piece Square Tables (PSTs). This method assign additional values to pieces based on their location on the board, reflecting positional strengths and weaknesses.For each piece type, there is a matrix that represents the board, where each square has a positional value
(V_p)= PST_{piece type}[rank][file]

Examples of Positional Advantages:

• Pawns: Advance in value as they move towards promotion; central pawns are more valuable than edge pawns.
• Knights: More effective in the center (e.g., d4, e5) where they control more squares.
• Bishops: Value open diagonals and avoid being blocked by their own pawns.
• Rooks: Prefer open files and the seventh rank, where they can pressure the opponent's position.
• Queen: Strongest in open positions with many available moves.

Mathematical Representation: For a piece i at position (r, f):
V_pi = PST_i[r][f]

The AI combines the material and positional evaluations into a comprehensive evaluation function. This function calculates a total score (E) representing the favorability of the current board state for the AI.

Evaluation Function Formula:
E = ( Σ_{i ∈ AI} ( M_i + V_pi ) ) − ( Σ_{j ∈ Opponent} ( M_j + V_pj ) )

Example Calculation:
AI has a knight (3 points) on e5 with V_p = +0.5.
Opponent has a bishop (3 points) on c8 with V_p = −0.2.

Total evaluation:
E = (3 + 0.5) − (3 − 0.2) = 3.5 − 2.8 = +0.7

Where:

• M_i: Material value of the AI's piece i.
• V_pi: Positional value of the AI's piece i.
• M_j: Material value of the opponent's piece j.
• V_pj: Positional value of the opponent's piece j.

The positive score indicates the AI has a slight advantage due to better piece positioning.

Strategic Planning: By calculating the evaluation score for possible moves, the AI can prioritize those that increase E, leading to material gains, improved positions, or both. This mathematical approach enables the AI to simulate future scenarios and make decisions that align with strategic objectives.

The Minimax Algorithm is the mathematical foundation of the AI's decision-making process in BattleChess. It allows the AI to evaluate potential moves by anticipating the opponent's responses and choosing moves that maximize its minimum gain.

The AI evaluates the game tree by assigning a value to each possible position (node) using the evaluation function E(s).

The Minimax value V(s) of a position s is defined recursively:
V(s) =
  if s is a terminal node:   V(s) = E(s);
  if it's AI's turn:   V(s) = max_{a ∈ A(s)} V(s');
  if it's player's turn:   V(s) = min_{b ∈ B(s)} V(s').
Where:

• s: Current game state.
• s': Game state resulting from move a or b.
• A(s): Set of possible moves for AI from state s.
• B(s): Set of possible moves for player from state s.
• E(s): Evaluation function assigning a numerical value to state s.

Steps in the Minimax Evaluation:

1. Generate Possible Moves: AI lists all legal moves from the current position.
2. Simulate Moves: For each move, AI simulates the move and generates the resulting position.
3. Evaluate Player's Responses: For each resulting position, AI assumes the opponent will play optimally and generates all possible responses.
4. Assign Scores: AI uses the evaluation function E(s) to assign scores to the terminal nodes (positions at the maximum depth or game-ending positions).
5. Backpropagate Scores: AI backpropagates the scores up the game tree, selecting the minimum score at player's turn and the maximum score at its own turn.
6. Select Move: AI chooses the move that leads to the position with the highest Minimax value.

Chess Move Example: Let's consider a initial position where player (White) has at least the following possible moves:

• M1: Pawn to e4
• M2: Knight to f3
• M3: Pawn to d4

The AI evaluates each move:

• After M1-> Opponent responds with:
  R1:Pawn to e5 (symmetrical position), evaluation: 0 or R2: Knight to c6, evaluation: +0.1 (slight advantage AI)
  Min value for M1: min(0, +0.1) = 0
• After M2-> Opponent responds with:
  R1:Pawn to d5, evaluation: +0.2 or R2: Pawn to e5, evaluation: +0.2
  Min value for M2: min(+0.2, +0.2) = +0.2
• After M3-> Opponent responds with:
  R1:Pawn to d5, evaluation: 0 or R2: Knight to f6, evaluation: +0.1
  Min value for M3: min(0, +0.1) = 0

The AI selects (Knight to f3) because it has the highest Minimax value of +0.2.

As the depth of the game tree increases, the number of possible positions grows exponentially, making it computationally intensive to evaluate every node. To address this, the AI uses Alpha-Beta Pruning to eliminate branches that cannot possibly affect the final decision.

Alpha α represents the best (highest) score that the maximizing player (AI) can guarantee, while Beta β represents the best (lowest) score that the minimizing player (opponent) can guarantee. The pruning condition is: if at any point α ≥ β, the AI stops evaluating further moves along that branch because the opponent will not allow that path to occur.

Suppose the AI is evaluating moves at depth 3 with the following scenario:

Depth 1 (AI's Move)-> M1: Move A
M2: Move B
Depth 2 (Opponent's Response):
(Evaluation Process with Alpha-Beta Pruning: Initialize α = -∞ and β = +∞.)

• After M1 -> Opponent responds with:
  R1: Response A1, evaluation: +1. Update β = min(+∞, +1) = +1.
  R2: Response A2, evaluation: 0. Update β = min(+1, 0) = 0
  Min value for M1: min(+1, 0) = 0. Update α = max(-∞, 0) = 0.
• After M2 -> Opponent responds with:
  (Before evaluating, check if α ≥ β; currently α = 0, β = 0; since α = β, pruning occurs.)
  The AI stops evaluating further moves under M2

The AI selects M1 because it has the higher Minimax value of 0 compared to M2 (not fully evaluated due to pruning).

Initial State: The Player (White) moves and it has all of top 5 recommendations at the same score. Why is the N g1 to f3 blue highlighted recommendation?

• Step 1: Initial Evaluation: The Minimax algorithm evaluates possible moves, considering that White wants to maximize the score, and Black minimizes it.
• Step 2: Alpha-Beta Pruning: The tree of possible moves is pruned where moves are clearly inferior, speeding up calculations by ignoring unnecessary branches.
• Step 3: Score Calculation: Each move is scored. The move N g1 to f3 scored -5, indicating a slight disadvantage for White. Its range (-290 to 182) represents possible outcomes with opponent responses. Despite sharing a score of -5 with other moves, this one offers more consistent outcomes.
• Step 4: Best Option: This move was chosen over others with the same score because its outcome range is more stable, avoiding potential risks in subsequent moves.

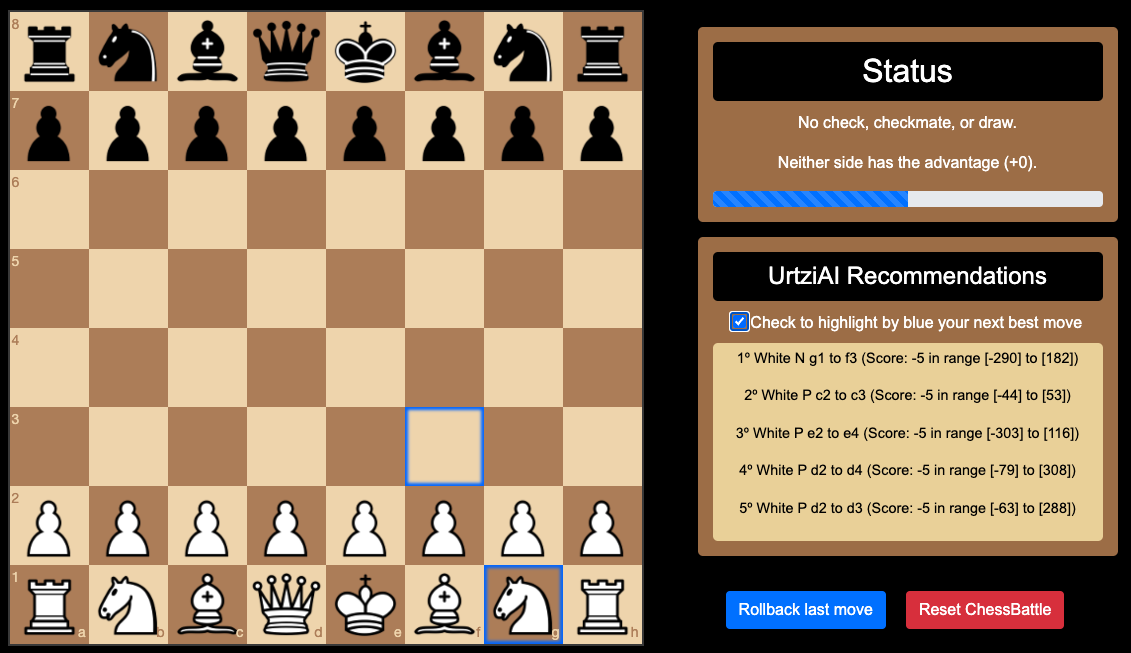
N g1 to f3 is the best move because it balances risk and opportunity better than the other options. First, it has a better best-case outcome (up to 182) than many other moves. The worst-case scenario (-290) is more manageable compared to some other moves, which have either extremely negative outcomes or narrower ranges that limit opportunities for gaining an advantage.

*Important* the reason why the top five recommendations all have the same score of -5 in the initial state is mainly due to two factors:

• Depth-3 Decision Tree: The AI's evaluation looks three moves ahead in the decision tree, which means it's evaluating the impact of the current move and the next two responses (one from each player). At such a shallow depth, the initial moves of white do not create a significant material or positional advantage over black, leading to similar evaluations.
• White's Starting Position: In chess, despite moving first, white is not always guaranteed an advantage. The score of -5 suggests that, even from the initial position, the AI estimates that white does not have a clear advantage and might be slightly at a disadvantage.

Black in Check State: The Player (White) only have two recommendations to skip it.

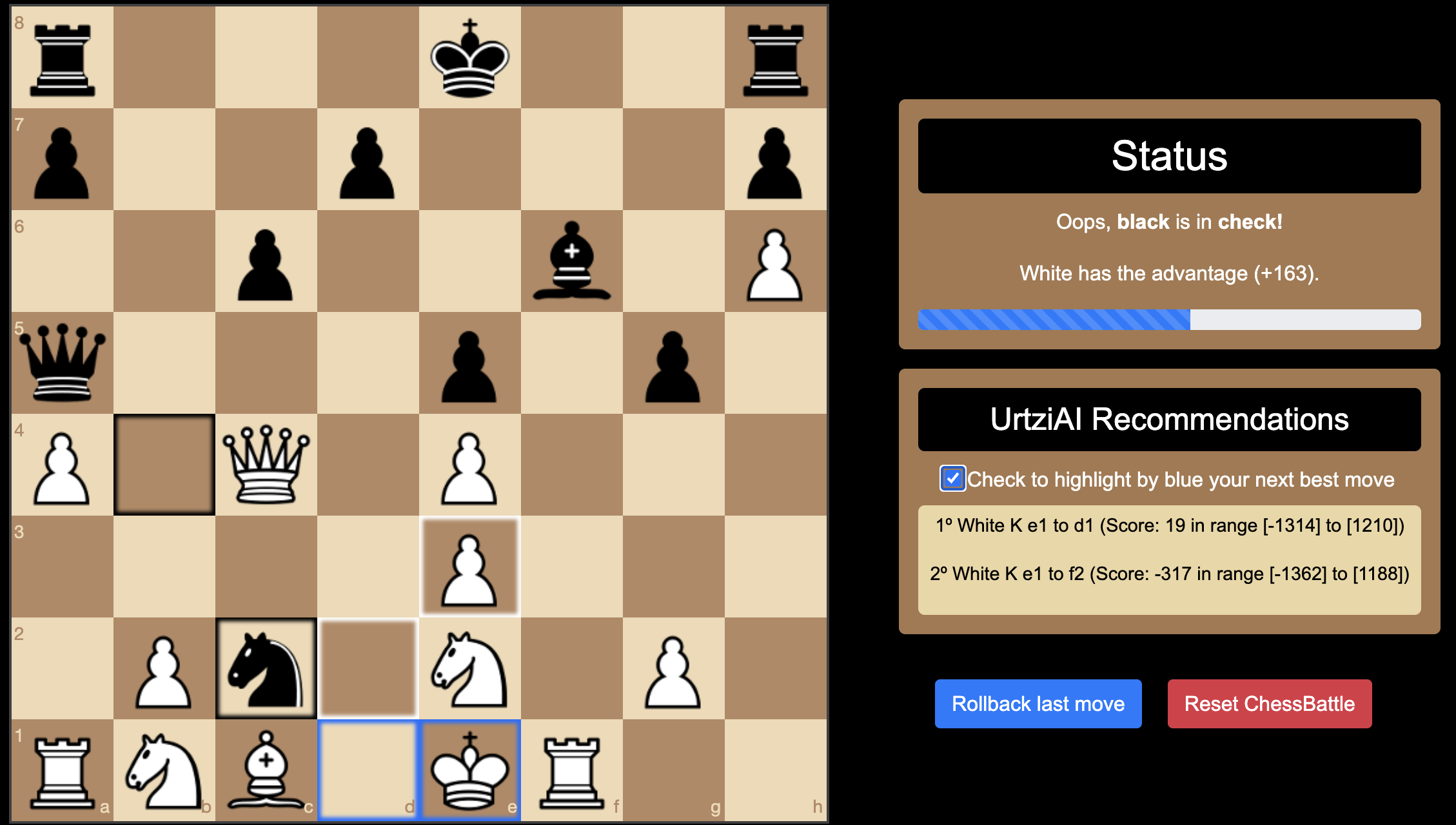
In this position, White is in check and must respond to get out of check.

• 1° White Ke1 to d1: This move yields a score of +19 in a range from -1314 to +1210. The positive score suggests that moving the king to d1 will effectively stabilize the position and maintain White's advantage.
• 2° White Ke1 to f2: This move results in a score of -317 within a range from -1362 to +1188. The negative score indicates a considerable risk, as this move leaves White in a much worse position compared to moving to d1.

Different Scores State: The Player (White) moves are each with a different score.

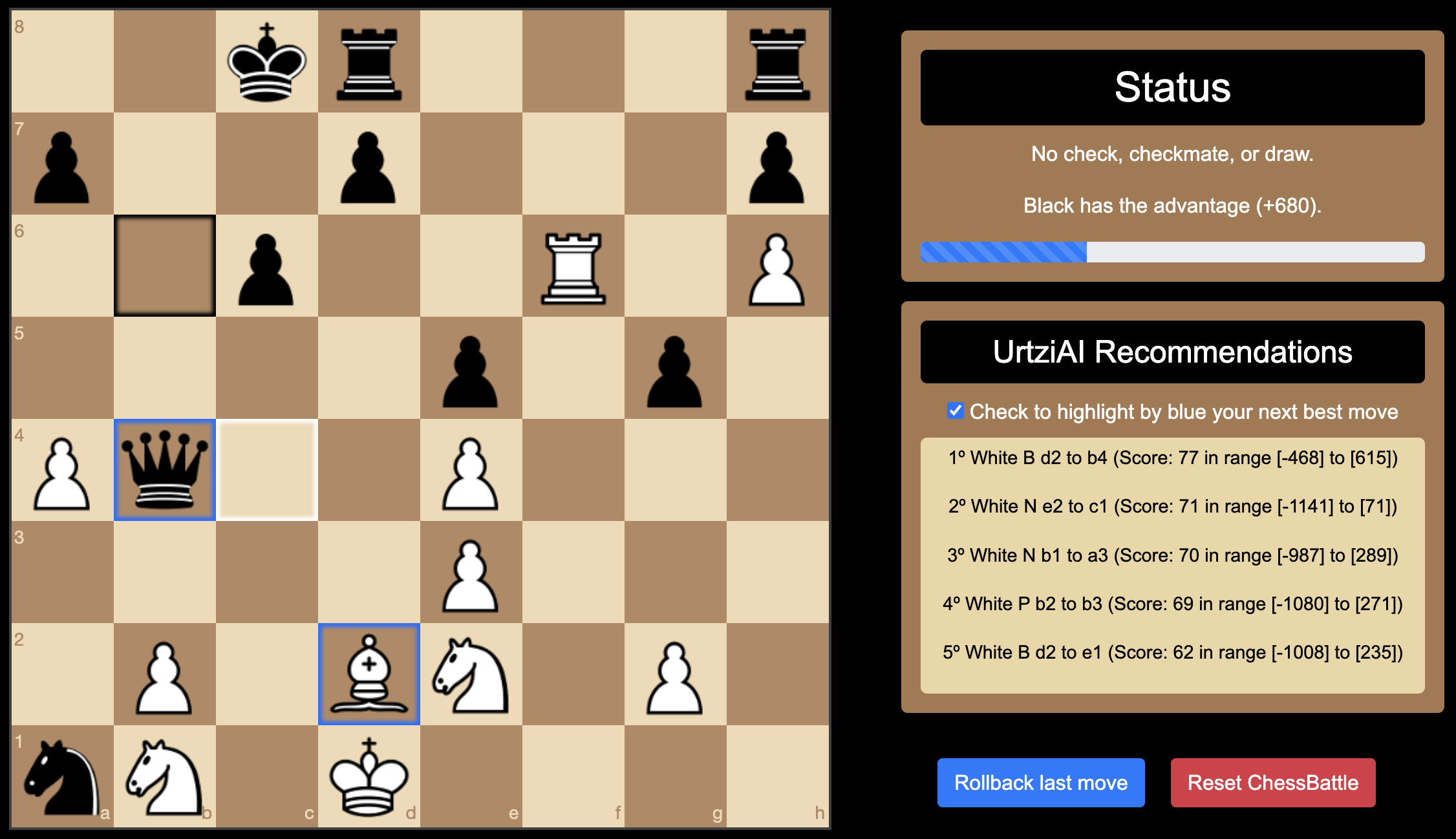
In this position, Black has a significant advantage, but White has several possible moves to reduce the impact. The scores differ because each move alters White's position in unique ways, influencing the material balance, control of the board, and future tactical opportunities.

Drawn State: The Player (White) is presented with multiple move options, but all have an equivalent score of 0.

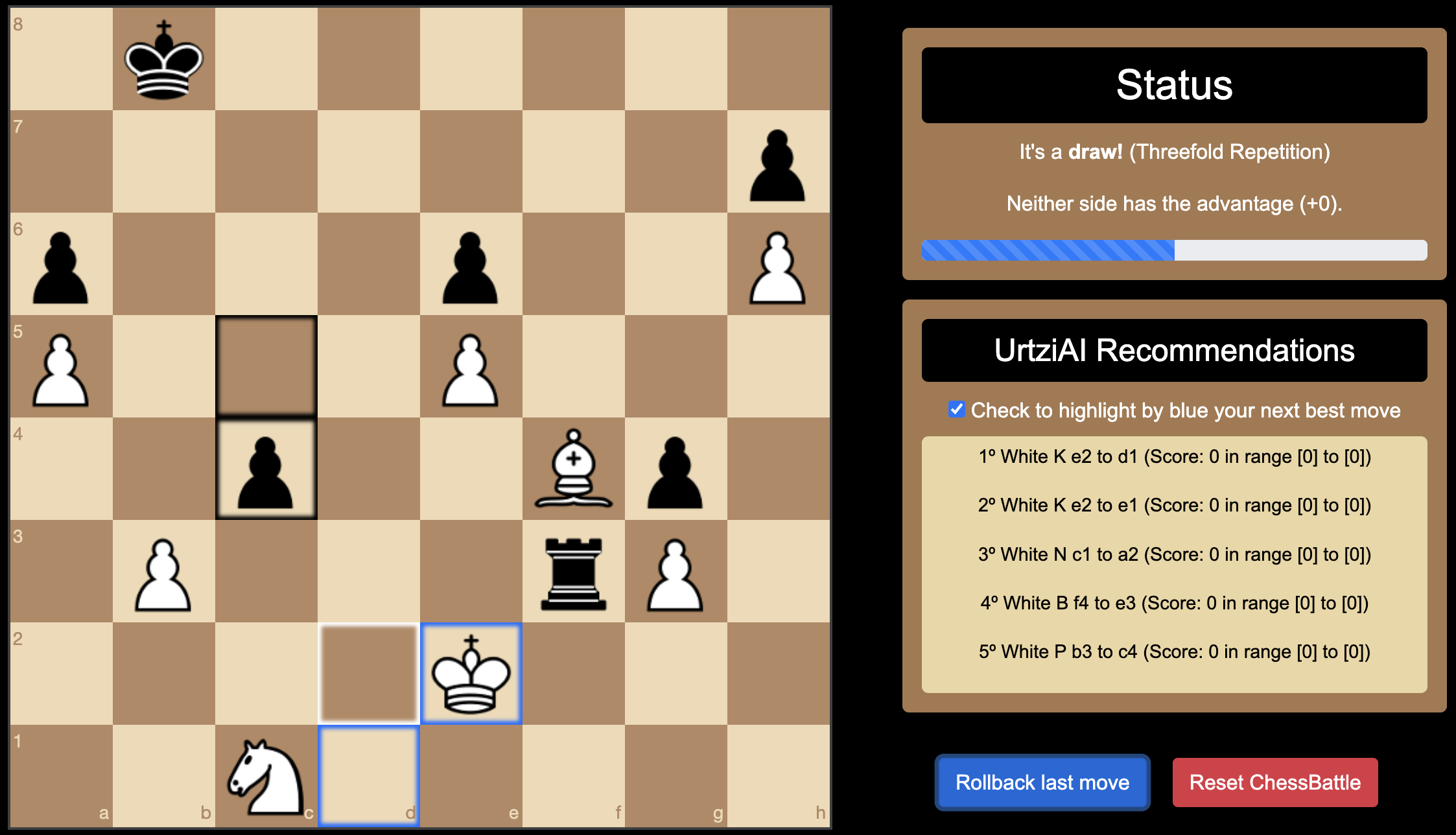
Neither side holds any advantage, as reflected by the score of +0 for all possible moves.

We have seen that in Game Theory, a zero-sum game is a situation where one player's gain is exactly equal to another's loss. Poker is a classic example of this because the amount won by one player is lost by the others. This competitive dynamic makes strategic decision-making crucial, as each player's actions directly impact the outcomes of others. However, what adds another layer of complexity is that Poker is also an imperfect information game, where players lack complete knowledge about the game state, often due to hidden information or randomness. In many card games, including Poker, players cannot see their opponents' cards, requiring decisions based on probabilities, intuition, and inference rather than certainty. This uncertainty adds complexity to the game, making strategy and adaptability essential for success.

The Counterfactual Regret Minimization (CRM) algorithm is a key method for making optimal decisions in imperfect information games like Poker. It works by minimizing "regret" over time, which measures how much better a player could have done by choosing different strategies. By iteratively updating strategies to minimize this regret, CRM converges toward a Nash Equilibrium, where no player can benefit from unilaterally changing their strategy. This approach allows players to systematically improve their decision-making process, even in the face of uncertainty and hidden information.

Typically, Counterfactual Regret Minimization algorithm would depict a game tree representing possible moves in a game like Poker. The game tree would show:

• Decision Nodes: Points where a player must choose an action.
• Chance Nodes: Points where randomness determines the outcome (like drawing a card).
• Edges: Possible actions or events leading to the next node.
• Regret Values: Annotations at each decision node showing how regret is calculated and updated over time.

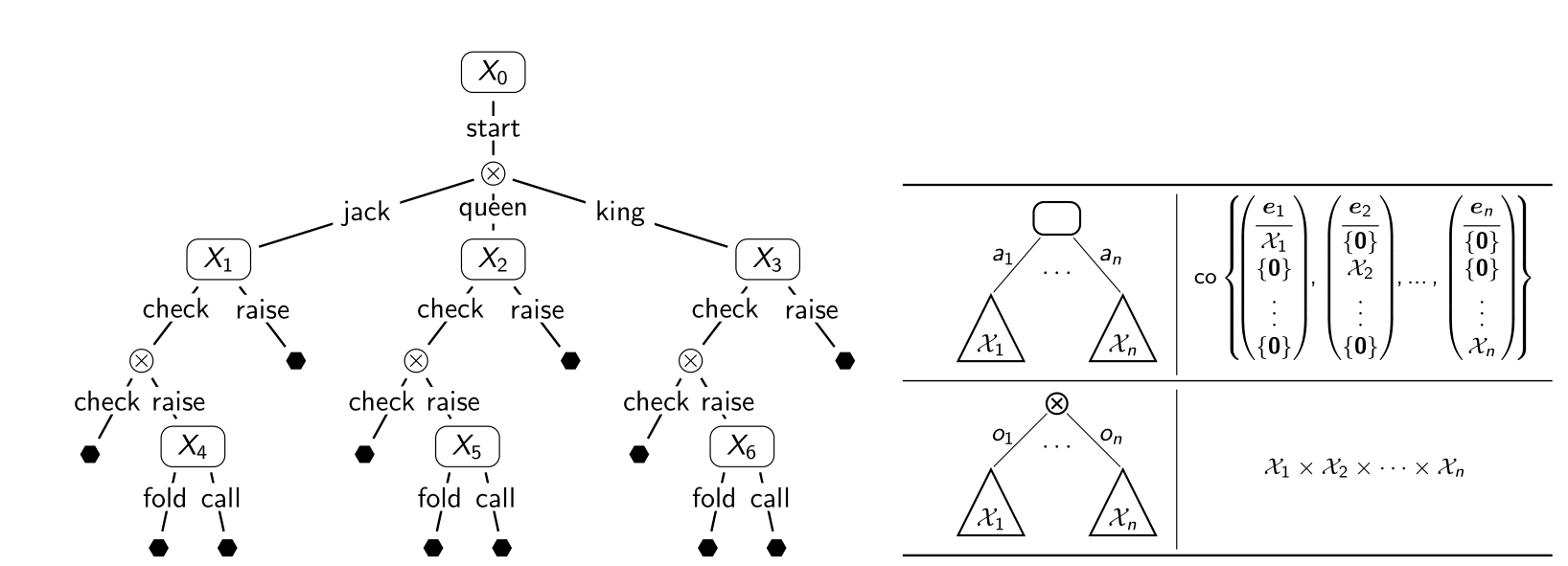
In Poker, CRM navigates the extensive game tree of possible moves and outcomes, accounting for all potential actions and counteractions. This allows players (or AI systems) to make decisions that effectively balance risk and reward, even when information is incomplete or hidden. The algorithm's ability to handle uncertainty makes it particularly suited for complex games like Poker.

This visual representation helps to understand how CRM navigates through the game tree, updating strategies at each node by minimizing regret based on the outcomes of simulated plays. By seeing how the algorithm iteratively adjusts decisions to converge towards an optimal strategy, the complexities of CRM become more approachable

Counterfactual Regret Minimization has been pivotal in advancing AI strategies for imperfect information games. By enabling systems to handle hidden information and adapt to opponents' behaviors, CRM has allowed AI to compete with (and even surpass) human experts in games like Poker.

Key AI Milestones:
Libratus vs. Top Professional Poker Players (2017)
Context: Libratus, developed by Carnegie Mellon University, defeated top human professionals in heads-up no-limit Texas Hold'em Poker.
How: Utilizing advanced CRM algorithms, Libratus effectively handled the vast number of possible game states and devised strategies that were both unpredictable and highly effective against human opponents.

Pluribus vs. Human Professionals (2019)
Context: Pluribus, a collaboration between Carnegie Mellon and Facebook AI, defeated multiple human professionals in six-player no-limit Texas Hold'em Poker.
How: Pluribus extended CRM techniques to multi-player settings, demonstrating that AI can outperform humans even in complex, multi-agent environments with imperfect information.

In conclusion, in zero-sum & imperfect information games, CRM enables players (and AI systems) to make optimized, strategic decisions despite uncertainty.

In BattlePoker, the AI's decision-making begins with assigning numerical values to each possible poker hand. These values represent the relative strength and probability of the hands, allowing the AI to quantify advantages or disadvantages during the game.

The standard hand rankings used are:

Poker hand rankings are based on the rarity and strength of each hand. For example, a Royal Flush is the highest-ranking hand due to its rarity, while a High Card is the lowest. Understanding these values is crucial for strategic decision-making in the game.

• High Card: Value = 1
• One Pair: Value = 2
• Two Pair: Value = 3
• Three of a Kind: Value = 4
• Straight: Value = 5
• Flush: Value = 6
• Full House: Value = 7
• Four of a Kind: Value = 8
• Straight Flush: Value = 9
• Royal Flush: Value = 10

Beyond assigning numerical values to hands, the AI evaluates the probabilities of various outcomes and models opponent behavior using statistical methods. This involves calculating the likelihood of certain hands being held by opponents based on available information and betting patterns.

Probability Calculations:
The AI calculates the probability of improving its hand or the chances that an opponent has a stronger hand.
(P(Event) = Number of Favorable Outcomes / Total Possible Outcomes)

Examples of Strategic Considerations:

• Pot Odds: Comparing the size of the pot to the cost of a contemplated call to determine if the call is profitable.
• Expected Value (EV): Estimating the average amount the AI expects to win or lose with a particular decision over time.
• Bluff Detection: Analyzing opponents' betting patterns to identify possible bluffs or strong hands.
• Position Advantage: Recognizing the benefits of acting later in a betting round, allowing the AI to gather more information before making a decision.

For example calculating pot odds:
Pot Odds = Potential Winnings / Cost to Call
If the pot odds are better than the odds of completing a winning hand, the AI may decide to call or raise.

Poker Game Example:
Suppose the AI considers two actions at a decision point: 'match' and 'raise'. The current regrets (R) are Rmatch = 5 and Rraise = 3. The strategy probabilities (S) are calculated as:

• Smatch = max(5, 0) / (5 + 3) = 0.625
• Sraise = max(3, 0) / (5 + 3) = 0.375


• The AI selects 'match' with probability 62.5% and 'raise' with 37.5%.

Suppose the AI chooses 'raise' and receives an actual reward Uactual = 10. It calculates counterfactual rewards (U) for all actions:

• Umatch = 8 (what it would have earned by matching)
• Uraise = 10 (the reward from raising)
• Rmatch = 5 + (8 - 10) = 3
• Rraise = 3 + (10 - 10) = 3
• Smatch = max(3, 0) / (3 + 3) = 0.5
• Sraise = max(3, 0) / (3 + 3) = 0.5

This adjustment reflects the updated regrets and shifts the strategy to consider both actions equally.

In summary, CRM minimizes regret by mathematically adjusting strategies based on the difference between actual and counterfactual rewards. This enables the AI to optimize its decision-making over time, adapting to the uncertainties of poker by learning from previous outcomes in precise quantitative terms.

Initial State: Pre-flop, the player is dealt a high-card ace, and Player 3 has bet $85.

• Step 1: Initial Evaluation: The AI calculates the player's hand strength as a high-card ace. The CFR algorithm evaluates potential actions—'check', 'match', 'raise', or 'all-in'—based on possible outcomes and opponent responses.
• Step 2: Regret Minimization: The CFR algorithm updates its strategy by reducing the likelihood of actions that have resulted in higher regret in the past and increasing the probability of those that minimized regret.
• Step 3: Action Calculation: The AI calculates that the player’s best options are 'check' or 'fold' given the strength of their hand and the size of the current pot ($40).
• Step 4: Best Option: The AI recommends checking (-0.42 reward), as raising or going all-in would introduce a high risk given the minimal value of the current hand.

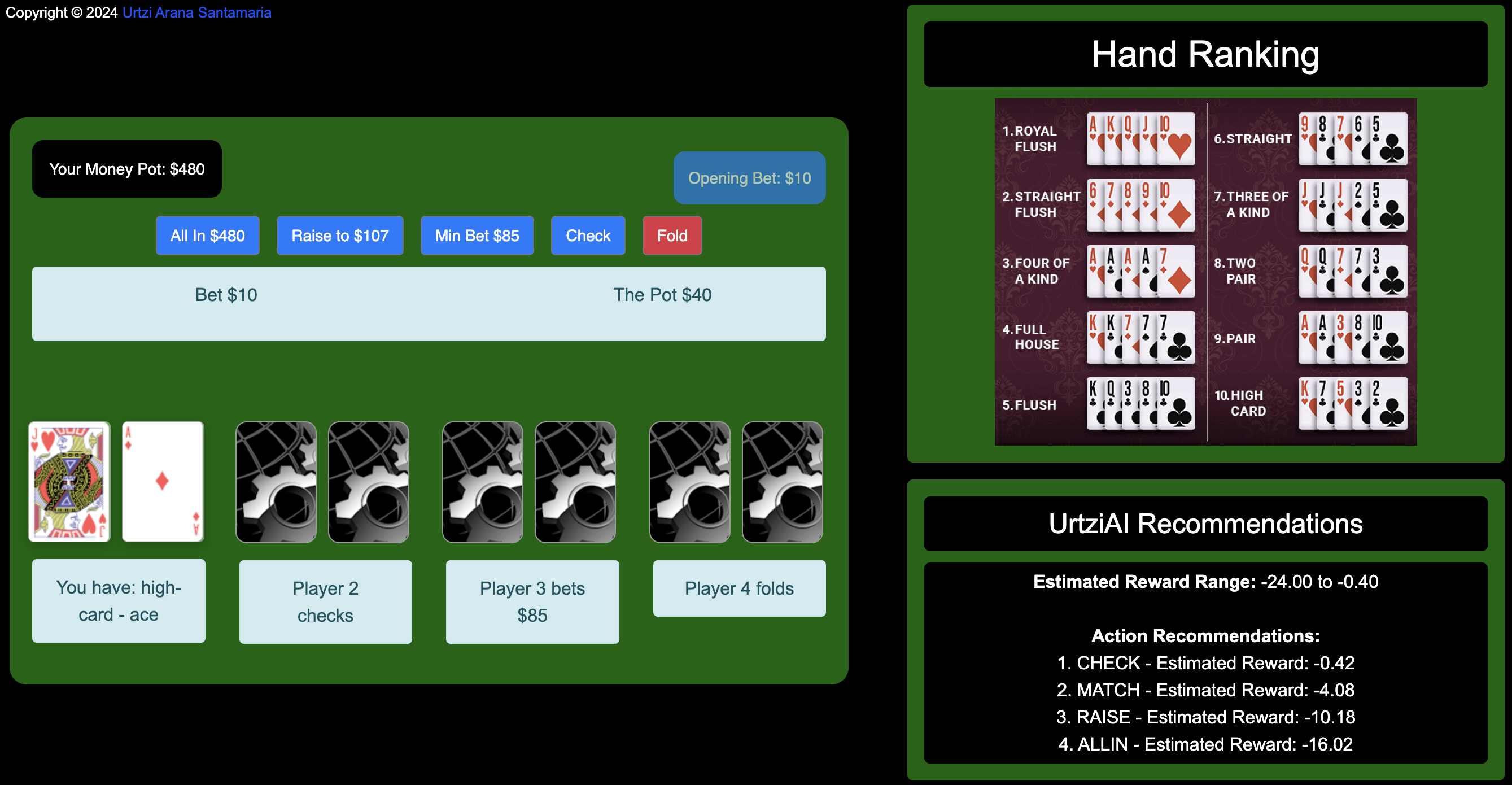
In this scenario, checking is the best move as it avoids unnecessary risk. The AI has calculated that more aggressive moves like 'raise' or 'all-in' would result in higher regret (score).

Betting After the Flop: The player now has a pair of jacks, and Player 3 has bet $108 increasing the pot.

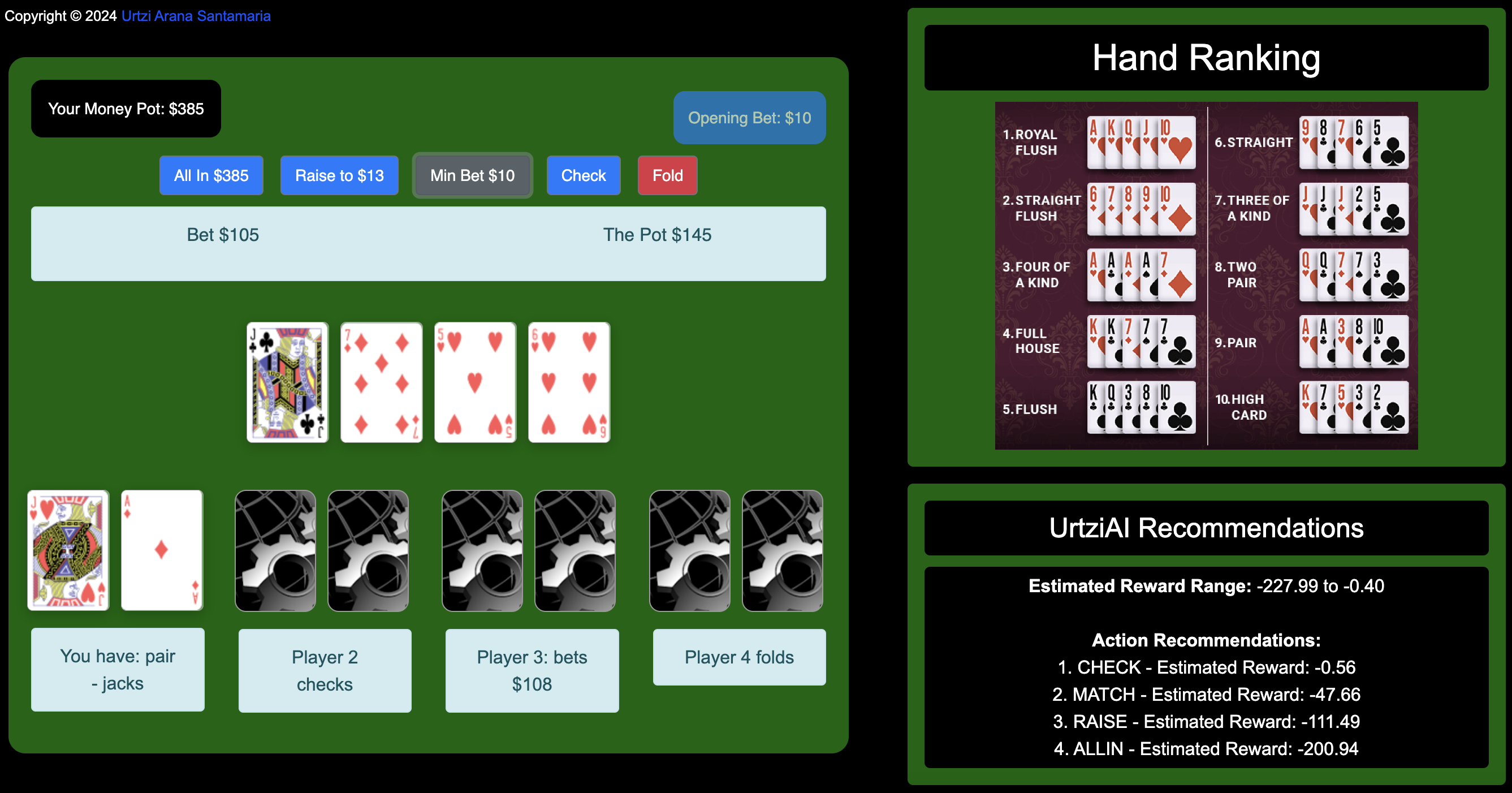
In this situation, the player’s hand has improved to a pair of jacks after the flop. The ranking of recommendations is based on minimizing risk while factoring in the player’s hand strength and Player 3's aggressive bet of $108.

• Check (-0.56): Safest option, avoiding unnecessary risk and limiting potential loss.
• Match (-47.66): Involves higher risk, as matching a large bet could lead to substantial loss.
• Raise (-111.49): Increases potential loss with limited upside based on the current hand strength.
• All-In (-200.94): Riskiest move, likely resulting in a significant loss due to the vulnerability of the hand.

The estimated reward range (-227.99 to -0.40) reflects the potential losses, with aggressive moves carrying greater risk and checking offering minimal loss.

Final Bet: The player has a pair of sixes and has gone in All-In.

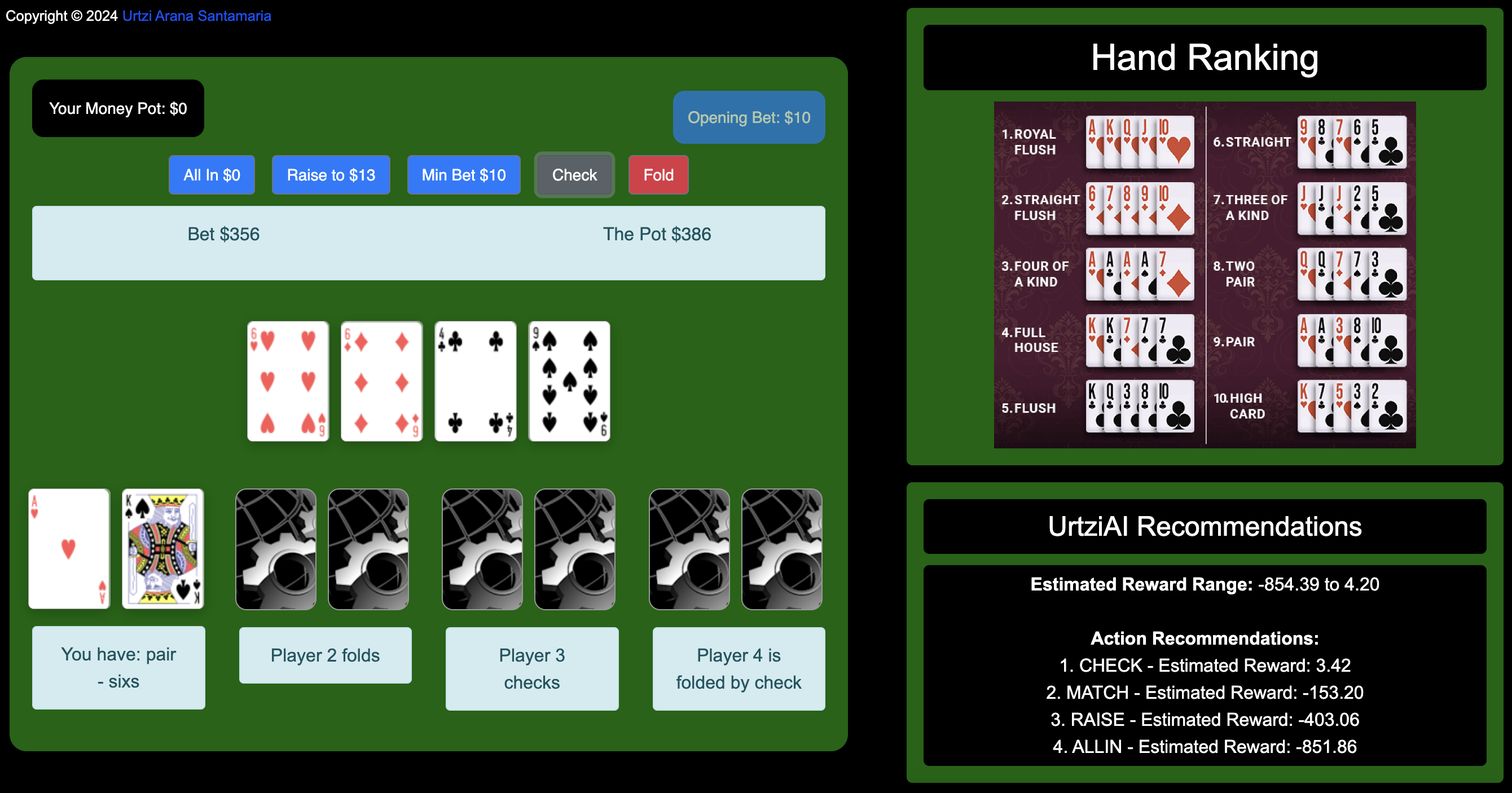
The reason the estimated reward range is so wide is due to the significant variation in outcomes based on different actions. The potential loss in aggressive actions like raising or going all-in reflects the vulnerability of the player's hand. If an opponent holds a stronger hand, the downside risk is very high, hence the negative values.

In conclusion, this range helps to illustrate the importance of careful decision-making. Although the check score is positive, which makes it the safest action, the lower end of the range shows that actions like raising or going all-in carry substantial risk. Understanding the width of this range is crucial for making an informed decision while aggressive plays might offer potential for higher rewards, they are also much more likely to result in large losses.

There are games like Risk and Catan which are renowned for their strategic depth and complex decision-making processes. These games are examples of zero-sum situations, where one player's gain is often balanced by the losses of others. They also involve imperfect information, as players may not know the exact strategies or resources of their opponents. The complexity arises from the vast number of possible game states and the iterative nature of gameplay, where each decision can significantly impact future options and outcomes. Players must plan multiple moves ahead, considering not only their own strategies but also predicting the actions of their opponents. This complexity requires players to constantly adapt their strategies, making these games both challenging and engaging.

To navigate this complexity, players often rely on heuristics or simplified models to make decisions. However, as the number of possible moves increases exponentially with each turn, traditional decision-making methods become less effective. This is where advanced algorithms like the Monte Carlo Tree Search (MCTS) come into play. MCTS allows for more efficient exploration of possible game states, enabling players (or AI systems) to make more informed decisions in complex iterative games.

MCTS builds a search tree incrementally and asymmetrically, focusing on the most promising moves. The algorithm consists of four main steps:

• Selection: Starting from the root node, select successive child nodes until a leaf node is reached.
• Expansion: If the leaf node is not a terminal node, expand it by adding one or more child nodes.
• Simulation: Run a simulation from the new node to a terminal state using random or heuristic policies.
• Backpropagation: Update the values of the nodes on the path from the new node to the root based on the simulation result.

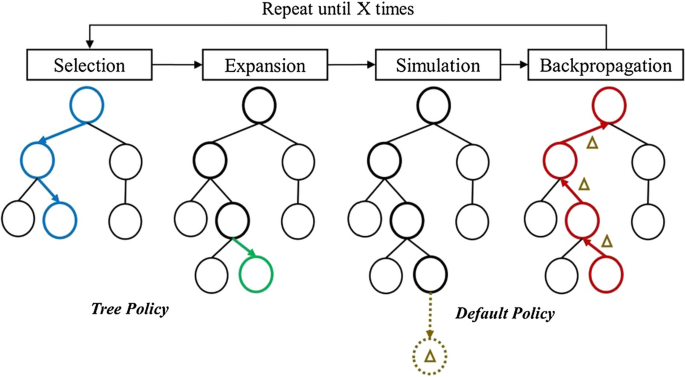
MCTS efficiently explores the vast game tree by simulating many possible future scenarios.

MCTS prioritizes certain branches of the game tree based on the results of simulations, effectively balancing exploration of new moves with exploitation of known favorable strategies. By focusing computational resources on the most promising moves, MCTS makes complex decision-making more tractable.

MCTS has significantly advanced AI strategies in complex iterative games. By efficiently handling the enormous number of possible game states and adapting to dynamic game environments, MCTS has enabled AI to perform at high levels in games previously dominated by human intuition and experience.

Key AI Applications:
AI in Chess Engines
Context: Modern chess engines like Leela Chess Zero utilize MCTS along with neural networks to make decisions.
How: It helps the AI explore potential moves more efficiently than traditional brute-force methods, leading to superior strategic play.
AI in Real-Time Strategy Games
Context: AI agents have been developed to play complex video games like StarCraft II.
How: MCTS enables the AI to handle real-time decision-making with imperfect information, considering a vast number of potential strategies and counter-strategies.

In conclusion, Monte Carlo Tree Search represents a significant mathematical advancement in AI and game theory. By utilizing probabilistic simulations and statistical analysis, MCTS efficiently navigates complex decision spaces in iterative games. Its ability to balance exploration and exploitation allows Artificial Intelligence systems to make optimized strategic decisions in environments with immense complexity and uncertainty.

In BattlePayRisk, we begin by revisiting the traditional rules of the classic Risk game. The objective is to conquer territories and eliminate opponents through strategic troop movements and battles. Each player starts with a set number of armies and territories, and the game progresses in turns consisting of reinforcement, attack, and fortification phases.

In the classic Risk control of entire continents grants bonus reinforcements,encouraging players to expand strategically.

Key elements of the traditional game include:

• Reinforcement Phase: Receive new troops based on the number of territories and controlled continents.
• Attack Phase: Declare attacks on adjacent enemy territories to expand your control.
• Fortification Phase: Move troops between your territories to strengthen positions.
• Objective: Eliminate all opponents.

In BattlePayRisk, you take on the role of a CEO of a payment company aiming to expand globally. The game transforms traditional Risk mechanics by integrating detailed country data, allowing you to analyze and decide where to invest based on economic indicators, expected incomes, and market tiers. Your strategic goal is to allocate resources efficiently, enter profitable markets, and outperform competitors in the global payments landscape.

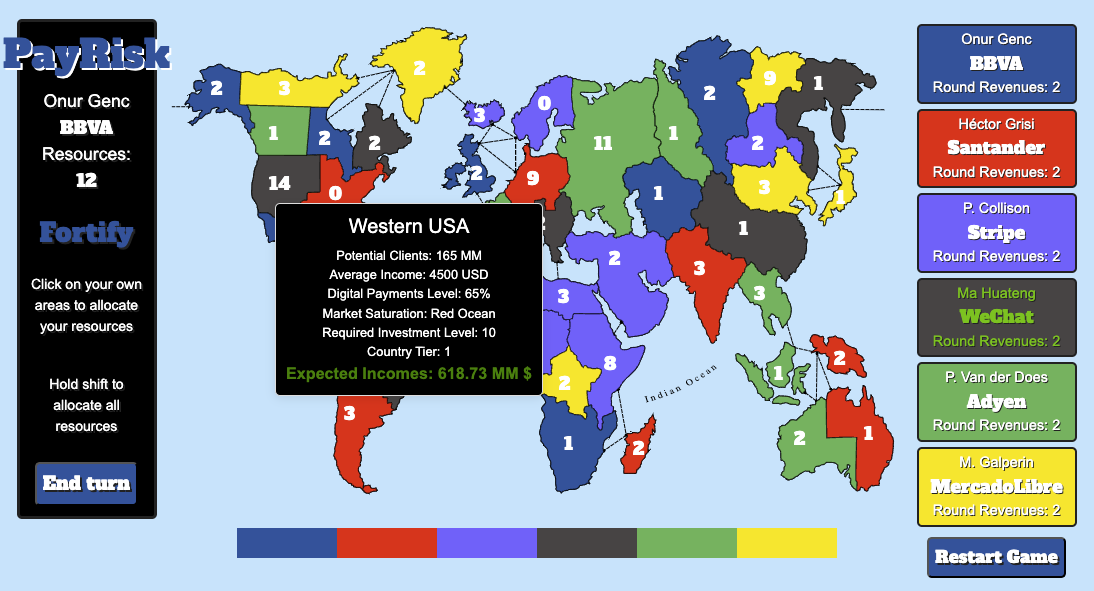
The world map is enriched with economic data for each country, such as potential customers, average salaries, digital payment penetration rates, competition levels, and investment requirements. This data-driven approach adds depth to your strategic decisions, simulating real-world business challenges.

Key adaptations in the game include:

• Country Analysis: Evaluate countries based on economic data to determine potential profitability.
• Expected Income Calculation: Use math to estimate net expected annual income from each market.
• Market Tiers: Classify countries into tiers based on expected incomes, guiding your expansion strategy.
• Strategic Recommendations: Receive AI-generated suggestions on where to allocate resources and when to enter or avoid markets.

BattlePayRisk introduces new goals centered around economic dominance and strategic investments. Players aim to control high-tier markets, maximize incomes, and outmaneuver opponents economically. To assist in making informed decisions, we utilize the Monte Carlo Tree Search (MCTS) algorithm.

The MCTS algorithm enhances gameplay by providing score ranges and recommendations for allocation and attack turns. It simulates several game states to evaluate the potential outcomes of different strategies.

How MCTS Works in BattlePayRisk:

• Selection: Starting from the current game state, MCTS selects promising moves based on prior statistics, balancing exploration of new strategies and exploitation of known successful ones.
• Expansion: It expands the game tree by adding new nodes representing possible actions, particularly focusing on high-tier countries.
• Simulation: For each expanded node, MCTS runs simulations (playouts) using algorithms that consider factors like expected income, investment costs, and competition levels. This step predicts the potential outcomes of different strategies.
• Backpropagation: The results of the simulations are propagated back up the tree, updating the statistics associated with each move. This process refines the MCTS's strategies are most effective.

By leveraging MCTS, BattlePayRisk offers a sophisticated AI assistant that aids in making complex strategic decisions. It mirrors how CEO might do math in real-world scenarios to guide company toward optimal outcomes.

As we have seen before MCTS operates through four main steps, we can understand them deeper right here:

1. Selection: Starting from the root node (current game state), the algorithm selects child nodes based on the Upper Confidence Bound formula until it reaches a leaf node.
2. Expansion: If the leaf node represents a non-terminal state (the game is not over), the algorithm generates possible child nodes (future moves) from this state.
3. Simulation (Rollout): The algorithm simulates a random playout from the expanded node to a terminal state, using heuristics to bias towards promising moves.
4. Backpropagation: The result of the simulation (win, loss, or score) is backpropagated through the selected nodes, updating their visit counts and total scores.

The key mathematical component in the selection step is the UCB formula:

UCB = (w_i / n_i) + c * sqrt(ln(N_i) / n_i)

Where:
• w_i: Total score of node i.
• n_i: Number of times node i has been visited.
• N_i: Total number of visits to the parent node of i.
• c: Exploration parameter (controls the trade-off between exploration and exploitation).

This formula ensures a balance between exploring new moves (high uncertainty) and exploiting moves with high average reward.

Example in BattlePayRisk: Let's consider the initial state of the game, where it must allocate resources (troops) to various countries.

MCTS algorithm has to evaluate and recommend specific moves, these recommendations could be split like:

• Allocation A: Deploy troops to India (Tier 1 market), high potential but high competition and investment cost.
• Allocation B: Focus on Brazil and Mexico (Tier 2 markets), balancing potential income and manageable competition.
• Allocation C: Invest in multiple Tier 3 countries for diversified growth with lower risk.

Advantages of MCTS in the Game:

• Efficient Search: Focuses computational resources on the most relevant parts of the game tree.
• Flexibility: Easily adapts to different stages of the game (e.g., fortification vs. battle phases).
• Incorporation of Heuristics: Allows biasing simulations towards more realistic and advantageous moves, such as targeting high marketTier countries.

Example of MCTS Optimization in Battle or Attack Phase: Now the CEO must decide if he/she wants to gain a new market or not.

• The AI considers attacking from a country with surplus troops to an adjacent enemy country with a high market potential.
• MCTS simulates the battle outcomes, considering the probability of success based on troop numbers and the strategic value of the target country.
• The algorithm assesses the long-term benefits, such as controlling a continent or reducing enemy influence.

How MCTS gets the Score Range Calculation in simulations:

• Territory Control: Points for each country owned, weighted by marketTier.
• Army Strength: Total troops contribute to defensive and offensive capabilities.
• Market Influence: Owning countries in higher tiers increases potential income.
• Continent Bonuses: Extra points for controlling all countries in a continent.
• Risk Assessment: Penalties for overextension or high enemy exposure.

By aggregating these factors, the AI evaluates the overall desirability of each move within the simulations.

"The Imitation Game" is a 2014 film directed by Morten Tyldum and starring Benedict Cumberbatch. The movie portrays the life of Alan Turing, a brilliant mathematician and logician who played a pivotal role in cracking the Enigma code during World War II. Turing's work not only contributed significantly to the Allied victory but also laid the groundwork for modern computing and artificial intelligence.

The story of Alan Turing exemplifies the profound impact that mathematical thinking can have on solving complex problems and making informed decisions. Leaders must be cautious not to fall into the trap of drawing conclusions without first engaging in thorough mathematical reasoning. Just as athletes must train consistently to perform at their best, so too must leaders practice and hone their analytical skills.

This dedication to practice aligns with the Greek concept of ethos, which refers to the character and credibility one builds through habitual actions. In leadership, ethos embodies the commitment to making decisions grounded in logic, ethics, and systematic analysis.

Moreover, as artificial intelligence continues to advance, our ability to leverage these technologies effectively hinges on our understanding of the underlying math. By doing the right math, we not only enhance our decision-making capabilities but also empower AI systems to perform optimally. This synergy between human insight and "machines" can drive innovation and success in ways previously unimaginable. Ultimately, leaders who embody the ethos of continuous learning and mathematical rigor position themselves and their organizations at the forefront of progress.

The Minimax algorithm is fundamental in AI for decision-making in two-player, turn-based games like chess. It aims to minimize the possible loss for a worst-case scenario by assuming that the opponent is also playing optimally.

Why Min and Max Alternate in Nodes:

• Max Nodes (AI's Turn): The AI aims to maximize its advantage, selecting moves that lead to the highest possible evaluation score.
• Min Nodes (Opponent's Turn): The AI assumes the opponent will try to minimize the AI's advantage, selecting moves that lead to the lowest possible evaluation score for the AI.
• This alternating pattern reflects the adversarial nature of the game, where each player tries to optimize their outcome while considering the best possible countermoves from the opponent.

In BattleChess, if both players use the best recommendations provided by the AI at the same search depth, the game theoretically results in a draw. This is because:

• Both players are making optimal moves based on the same evaluation function and depth.
• The Minimax algorithm ensures that neither player can unilaterally force a win if the opponent plays optimally.
• The game reaches a state of equilibrium, reflecting a perfectly balanced strategy from both sides.

This scenario demonstrates the concept of Nash Equilibrium in game theory, where no player can gain an advantage by changing their strategy unilaterally.

In BattleChess you have a one level advantage.

In BattlePoker, the AI uses the Counterfactual Regret Minimization (CFR) algorithm to make decisions that balance risk and reward.

Importance of Comparing Score Ranges for Each Decision:

- Each possible action (check, match, raise, all-in) has an associated range of expected rewards based on various factors like hand strength, pot size, and number of opponents.
- The AI calculates estimated rewards for each action, considering both the minimum and maximum possible outcomes.
- Higher risk actions (like raising or going all-in) have wider score ranges due to greater variance in possible outcomes.

Using Score Ranges to Make Decisions:

- Players can use the AI's recommended strategies and score ranges to inform their own decisions.
- By understanding the expected reward range for each action, players can assess their risk tolerance and choose actions that align with their strategy.
- For instance, a player who prefers safer play might choose actions with narrower score ranges and lower risk, while a more aggressive player might opt for actions with higher potential rewards despite the increased risk.

By continuously updating regrets and strategies through CFR, the AI adapts to the game's dynamics, providing players with informed recommendations that reflect both potential rewards and risks.

Looking ahead, integrating advanced AI algorithms into a game similar to Catan can create a rich, strategic experience adapted to business scenarios, such as competing in the global payments market.

Imagining Catan with Business Goals in the Global Payments Market:
- Game Concept: Players act as CEOs of international payment companies, competing to expand their networks, acquire resources, and achieve market dominance in the global payments industry.
- Resource Management: Instead of traditional resources like brick or wheat, players collect assets such as technology patents, regulatory licenses, customer data, and strategic partnerships.
- Building and Expansion: Players establish offices (settlements) and data centers (cities) in key financial regions worldwide, aiming to optimize transaction processing and customer reach.
- Trading and Negotiation: Players engage in deals to exchange assets, form alliances, or negotiate market access, reflecting real-world business negotiations.

Different algorithms role:

Minimax/Alpha-Beta: Plan expansions and block competitors by analyzing potential moves
CFR: Adjust negotiation strategies based on players' past behaviors, optimizing trade deals and alliances.
MCTS: Simulate long-term market trends and competition outcomes to inform strategic decisions.